宅男教你如何觀察正妹的內褲(胖次)
宅男教你如何觀察正妹的內褲(胖次)
突然發現對面坐著一個超甜美的正妹..
迷你裙下修長勻稱的雙腿..
要是能偷瞄到一點點..
不知道該有多好..
這樣的情況應該是屢見不鮮了..
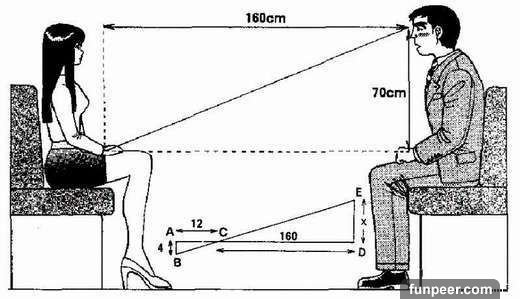
且讓我們假設女孩雙膝並隆的點和裙子上緣距離4公分..
而裙襬到小褲褲之間的距離是12公分..
那麼從側面看來..
目標區域和裙子就會形成一個直角三角形abc
如果"觀察者"的雙眼e正好在bc線段的延長線上..
那麼b點就會落在他的視野內..
如果我們做一條過e並垂直於ac線段延長線的直線de的話.
直角三角形dec就會和直角三角形abc相似
在△abc中..
ab的長度是ac的三分之一..
因此在abc裡..
de的長度也應該是dc的三分之一..
又因為dc是觀察者的眼睛與裙子之間的水平距離..
假設這個距離是1.6公尺..
那麼de的長度(眼睛距離裙襬的高度)x就是53.3公分..
不過一個身高170公分的觀察者在採取普通坐姿時..
他的眼睛與裙襬之間卻會有70公分的差距..
換句話說..
他必須要把頭向下低個17公分..
而且為了達成這個目標..
得要讓屁股向前挺出45公分才行..
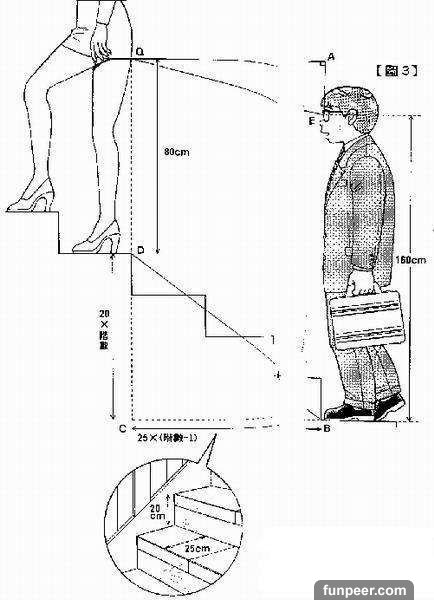
無論走到哪裡..
百貨公司.?.
隨時都會看到短裙美女上下樓梯的景象..
看著白皙的雙腿隨著步伐不斷交錯..
心裡不禁暗想..
要是我緊跟在她後面.
一定有機會看到..
不過..
想一窺裙底機密也是有技巧的喔!!
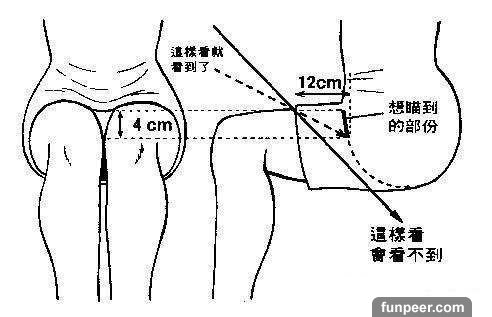
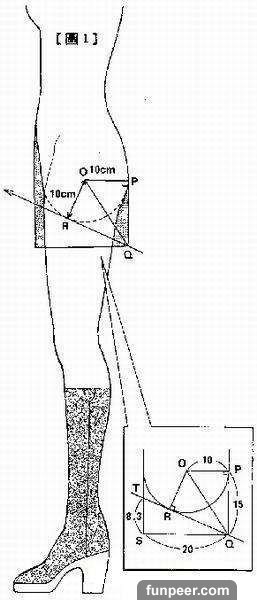
短裙的內部狀況大致就跟下圖(內附一)所示一樣
一般"觀察者"想看的地方..
其實是半徑10公分的半球體部分..
而裙子則與半球體相切並以向下15公分的剪裁..
巧妙地遮住了觀察者的視線..
直角三角形opq和orq是全等的.
如果將qr線段(也就是觀察者視線)延長並做出另一個直角三角形tsq..
那我們可由計算知道它的高是8.3公分..
tsq的高是底的0.415倍..
所以..
觀察者如果想看到裙底風光..
最低限度是讓視線的仰角大於角tqs..
也就是高和底的比值要大於0.415倍..
一般"觀察者"想看的地方..
其實是半徑10公分的半球體部分..
而裙子則與半球體相切並以向下15公分的剪裁..
巧妙地遮住了觀察者的視線..
直角三角形opq和orq是全等的.
如果將qr線段(也就是觀察者視線)延長並做出另一個直角三角形tsq..
那我們可由計算知道它的高是8.3公分..
tsq的高是底的0.415倍..
接下來..
我們就要討論△aeq的問題..
假設觀察者(身高170)眼睛的高度是160公分..
而裙襬高度是80公分..
因為眼睛高度比裙襬高度大80公分..
所以裙襬與眼睛的高度差距(線段ae)..
就比樓梯的高低差距(線段cd)小80公分..
因此直角三角型aeq的高和底可用以下兩個式子來表示..
高:ae=20×階數-80
底:qa=25×(階數-1)
高和底則須滿足這個式子:ae≧oa×0.415
因此直角三角型aeq的高和底可用以下兩個式子來表示..
高:ae=20×階數-80
底:qa=25×(階數-1)
高和底則須滿足這個式子:ae≧oa×0.415
我們針對不同的階梯差距列一張表:
│階數│1│2│3│4│5│6>│7│8│
│ae│-60│-40│-20│0│20│40│>60│80│
│qa│0│25│50│75│100│125│>150│175│
│比率│*│-1.6│-0.4│0│0.2│0.32│>0.4│0.457│
其中ae是負值的情況..
就表示裙襬問至還在眼睛下方..
所以在階梯差距小於4時..
觀察者是完全看不到裙子底下的..
但是..
當階梯數增加到5或6的時候..
喔喔~~~~就快看到啦!!
等到階梯差到了8時..
0.415的障礙也就被破解啦!!
當然..
這個差距愈大..
視野也就愈寬廣..
不過可以看到的風光也會愈來愈小..
PS:這不是一般人能看的懂的!!!!!
卡提諾宅宅歡迎你 本帖最後由 真冬 於 2013-5-20 16:18 編輯
|
本篇 |
不想錯過? 請追蹤FB專頁! |
| 喜歡這篇嗎?快分享吧! |
相關文章
說好的呢?